• 1. Dellen
• 2. In Pixel auflösen
• 3. Kachelspiegelung
• 4. Kristallisieren
• 5. Milchglas
• 6. Morphologie
• 7. Polarinvertierung
• 8. Spirale
• 9. Wölbung

Mit den Effekten zum Verzerren wird in Paint.Net ein bestehendes Bild verändert. Auf eine leere Grafik haben diese Effekte keine Wirkung. Die Effekte zum Verzerren erscheinen im Untermenü genau in der hier aufgeführten Reihenfolge, das heißt: alphabetisch sortiert. Das bedeutet aber auch, dass ggf. die Reihenfolge in einer anderen Sprache abweichend ist.

Der Untermenüpunkt Verzerren im Menü Effekte sieht so aus:

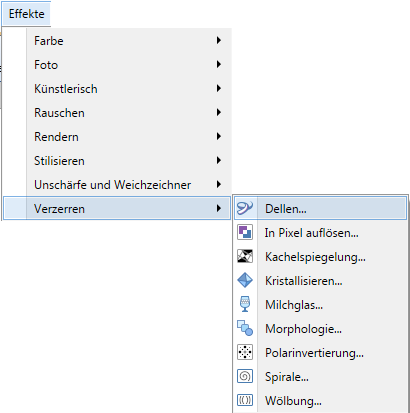
Wie man erkennen kann gibt es 9 Einzeleffekte

• Dellen
• In Pixel auflösen
• Kachelspiegelung
• Kristallisieren
• Milchglas
• Morphologie
• Polarinvertierung
• Spirale
• Wölbung

Dazu werden im Folgenden Beispiele dargestellt.

Dellen

Mit den Parametern

• Skalierung 25
• Brechung 125
• Grobheit 4
• Spannung 3
• Qualität 2

ergibt sich das folgende Bild:

In Pixel auflösen

Mit dem einzigen Parameter Kantenlänge 10

ergibt sich das folgende Bild:

Kachelspiegelung

Mit den Parametern

• Winkel 30
• Kachelgröße 40
• Biegung 8
• Qualität 2

ergibt sich das folgende Bild:

Kristallisieren

Mit den Parametern

• Zellgröße 8
• Qualität 2

ergibt sich das folgende Bild:

Milchglas

Mit den Parametern

• Maximaler Punktradius 12
• Minimaler Punktradius 8
• Glättung 6

ergibt sich das folgende Bild:

Morphologie

Mit den Parametern

• Breite 26
• Höhe 5
• Modus Erodieren

ergibt sich das folgende Bild:

Polarinvertierung

Mit den Parametern

• Stärke 0,01
• Versatz 0,07 und -0,18 (der Versatz ist natürlich immer bildspezifisch )
• Randverhalten Zyklisch wiederholen
• Qualität 2

ergibt sich das folgende Bild:

Spirale

Mit den Parametern

• Stärke / Richtung 15
• Größe 1
• Mitte 0 und 0 (der Versatz ist natürlich immer bildspezifisch)
• Qualität 2

ergibt sich das folgende Bild:

Wölbung

Bei diesem Effekt kann man einen Mittelpunkt setzen, der dann das Zentrum für den Effekt bildet.

Mit den Parametern

• Wölbung 100
• Mittig 0,14 und -0,23 (der Versatz ist natürlich immer bildspezifisch)

ergibt sich das folgende Bild: